高数笔记一:关于「函数极限和连续」的几种典型问题的处理方法
复习「函数极限和连续」相关知识点和例习题时,遇到了4种需要注意的情况:
1 复合函数和积分的等价无穷小问题
2 含$\lim\limits_{n\to\infty}$函数的间断点问题
3 函数极限的存在性问题
- 3.1 具体型
- 3.2 抽象型
4 反函数问题
下面对这4种情形进行讨论。
1 复合函数和积分的等价无穷小问题
首先来看这个例题(摘自《18讲》P15习题1.13)
已知当$x\to0$时,$\mathnormal{f(x)}\sim\mathnormal{ax^m}$,$\mathnormal{g(x)}\sim\mathnormal{bx^n}$,且$f(x)$,$g(x)$,$a$,$b$均不为0,证明$$f[g(x)]\sim\mathnormal{ab^mx^{mn}}(x\to0).$$
【证】$\lim\limits_{x\to0}\dfrac{f[g(x)]}{x^{mn}}=\lim\limits_{x\to0}{\dfrac{f[g(x)]}{a[g(x)^m]}\cdotp\dfrac{[g(x)]^m}{(bx^n)^m}\cdotp\mathnormal{ab^{mn}}}=ab^m$,故$$f[g(x)]\sim\mathnormal{ab^mx^{mn}}(x\to0).$$
通过等价无穷小比阶+连乘消元的方式证明,避免了更加繁琐的、列写高阶无穷小的等式证明方法。
可以得出的结论是:复合函数的等价无穷小可以通过把自变量函数以等价无穷小的形式代入复合函数的等价无穷小中所得。
值得注意的是,自变量$x$的阶数是乘积关系而非加和关系。
利用这个结论,我们来看下一个例题(摘自《660题》P11习题21)
已知当$x\to0$时$F(x)=\int_{0}^{x-sinx}\text{ln}(1+t)\text{d}t$是$x^n$的同阶无穷小,则$n$=____.
【解】$F(x)=\int_{0}^{x-sinx}\text{ln}(1+t)\text{d}t$由$F(x)=\int_{0}^{u}\text{ln}(1+t)\text{d}t$和$u=x-sinx$复合而成,当$x\to0$时,$\text{ln}(1+t)\sim{x}$,所以$F(x)=\int_{0}^{u}\text{ln}(1+t)\text{d}t$与$x^2$同阶,而$x-sinx\sim{\dfrac{1}{6}x^3}$,由结论可知,$F(x)=\int_{0}^{x-sinx}\ln(1+t)\text{d}t$是$x$的$2\times3=6$阶无穷小。
可见对于选填小题,利用复合函数的等价无穷小结论可以快速准确地得出答案。如果是解答题的情况,采用洛必达求取n值,则会相对复杂。
2 含$\lim\limits_{n\to0}$函数的间断点问题
引例(摘自《1000题》P7习题6)
设函数$f(x)=\lim\limits_{n\to\infty}\text{cos}^n\frac{1}{n^x}(0<x<+\infty)$,则$f(x)$在其间断点处的值等于______.
【解】当$n\to\infty$时,$$\text{ln}\Big[1+\Big(\text{cos}\frac{1}{n^x}-1\Big)\Big]\sim \text{cos}\frac{1}{n^x}-1\sim -\frac{1}{2}\Big(\frac{1}{n^x}\Big)^2=-\frac{1}{2}\cdotp\frac{1}{n^{2x}},$$
所以$\lim\limits_{n\to\infty}\text{cos}^n\frac{1}{n^x}=e^{\lim\limits_{n\to\infty}n\text{ln}[1+(\text{cos}\frac{1}{n^x}-1)]}=e^{-\frac{1}{2}\lim\limits_{n\to\infty}\frac{1}{n^{2x-1}}}$,因此$$f(x)\begin{cases}
0,&0<x<\dfrac{1}{2},\\\dfrac{1}{\sqrt{e}},&x=\dfrac{1}{2},\\1,&x>\dfrac{1}{2}.
\end{cases}$$
故$f(x)$在其定义区间内由唯一的间断点$x_0=\dfrac{1}{2}$,且$f(x_0)=\dfrac{1}{\sqrt{e}}$.
可见在处理含有$\lim\limits_{n\to\infty}$函数的间断点问题时,可以分为以下几个步骤:
1.找到原函数的所有间断点,这个过程在面对无法直观判断间断点的函数时可能需要对原函数进行等价无穷小的化简
2.在间断点划分出的连续区间内,消除含有n的部分,将原函数化简为分段函数的形式
3.对间断点进行类型判断
解题关键和难点步骤在于第1步找出所有的间断点。一般情况下可以利用如下2种判断依据:
1.使分母为0的无意义点
2.与n相关并影响函数具体形式的点
循着这个思路和方法,我们来看下一个例题(摘自《1000题》P6习题37)
已知$f(x)=\lim\limits_{n\to\infty}\dfrac{x^{2n-1}+ax^2+bx}{x^{2n}+1}$是连续函数,求$a$,$b$的值.
【解】当$x=1$时,$f(x)=\lim\limits_{n\to\infty}\dfrac{x^{2n-1}+ax^2+bx}{x^{2n}+1}=\dfrac{1+a+b}{2}$;
当$|x|<1$时,$f(x)=\lim\limits_{n\to\infty}\dfrac{x^{2n-1}+ax^2+bx}{x^{2n}+1}=\dfrac{ax^2+bx}{1}=ax^2+bx$;
当$|x|>1$时,$f(x)=\lim\limits_{n\to\infty}\dfrac{x^{2n-1}+ax^2+bx}{x^{2n}+1}=\dfrac{\frac{1}{x}+a\frac{1}{x^{2n-2}}+b\frac{1}{x^{2n-1}}}{1+\frac{1}{x^{2n}}}=\dfrac{1}{x}$;
当$x=-1$时,$f(x)=\lim\limits_{n\to\infty}\dfrac{x^{2n-1}+ax^2+bx}{x^{2n}+1}=\dfrac{-1+a-b}{2}$;
于是$f(x)=\begin{cases}
ax^2+bx,&|x|<1,\\\dfrac{1}{x},&|x|>1,\\\dfrac{1+a+b}{2},&x=1,\\\dfrac{a-b-1}{2},&x=-1.
\end{cases}$只需讨论分断点处的连续性:在$x=1$处,有$\lim\limits_{x\to1^+}f(x)=\lim\limits_{x\to1^+}\frac{1}{x}=1$,$\lim\limits_{x\to1^-}f(x)=\lim\limits_{x\to1^-}(ax^2+bx)=a+b$,$f(1)=\frac{1+a+b}{2}$.要使$f(x)$在$x=1$处连续,则$a+b=1$;
在$x=-1$处,有$\lim\limits_{x\to(-1)^-}f(x)=\lim\limits_{x\to(-1)^-}\frac{1}{x}=-1$,$\lim\limits_{x\to(-1)^+}f(x)=\lim\limits_{x\to(-1)^+}(ax^2+bx)=a-b$,$f(-1)=\frac{a-b-1}{2}$.要使$f(x)$在$x=-1$处连续,则$a-b=-1$.
综上可得,当$a=0$,$b=1$时,$f(x)=\lim\limits_{n\to\infty}\dfrac{x^{2n-1}+ax^2+bx}{x^{2n}+1}$是连续函数.
3 函数极限的存在性问题
3.1 具体型
若给出具体函数求极限,但极限不满足洛必达法则三个条件中的至少一个:(1)$“\frac{0}{0}”$型或$“\frac{\infty}{\infty}”$型;(2)分子分母均可导;(3)结果为$0$,$c(c\ne0)$,$\infty$,则洛必达法则失效,可考虑用夹逼准则.
下面来看这个例题(摘自《18讲》P10例1.14)
设函数$S(x)=\int_{0}^{x}|\text{cos}\space t|\text{d}t.$
(1)当$n$为正整数,且$n\pi\leqslant x<(n+1)\pi$时,证明$2n\leqslant S(x)<2(n+1)$;
(2)求$\lim\limits_{x\to+\infty}\frac{S(x)}{x}.$(1)【证】因为$|\text{cos}\space x|\geqslant0$,且当$n\pi\leqslant x<(n+1)\pi$时,$$\int_{0}^{n\pi}|\text{cos}\space x|\text{d}x\leqslant S(x)<\int_{0}^{(n+1)\pi}|\text{cos}\space x|\text{d}x.$$
又因为$|\text{cos}x|$是以$\pi$为周期的函数,在每个周期上积分值相等,所以$$\int_{0}^{n\pi}|\text{cos}\space x|\text{d}x=n\int_{0}^{\pi}|\text{cos}\space x|\text{d}x=2n,$$$$\int_{0}^{(n+1)\pi}|\text{cos}\space x|\text{d}x=2(n+1),$$
因此,当$n\pi\leqslant x<(n+1)\pi$时,有$2n\leqslant S(x)<2(n+1).$
(2)【解】由(1)知,当$n\pi\leqslant x<(n+1)\pi$时,有$\dfrac{2n}{(n+1)\pi}<\dfrac{S(x)}{x}<\dfrac{2(n+1)}{n\pi}.$令$x\to+\infty$,则$n\to\infty$,由夹逼准则得$\lim\limits_{x\to+\infty}\dfrac{S(x)}{x}=\dfrac{2}{\pi}.$
这种情形下,使用夹逼准则的要点在于:
1.利用自变量的范围推算题设所要求的值范围,一般可能需要利用周期函数的特性来确定这个范围
2.再次利用自变量的范围进行放缩和夹逼
循着这个思路,我们来看下一个例题(摘自《18讲》P16习题1.15)
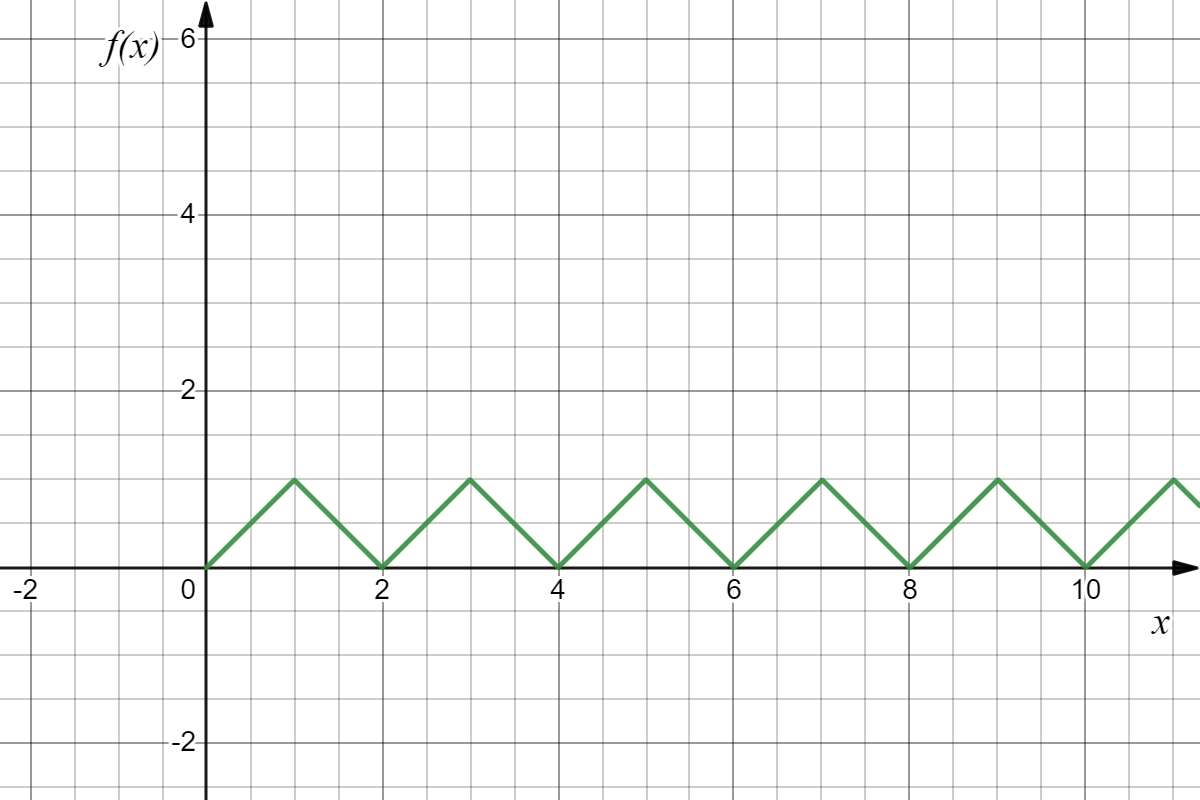
设$x\geqslant0$,记$x$到$2k$的最小距离为$f(x),k=0,1,2\cdots.$
(1)证明$f(x)$以2为周期,并写出其在$[0,2]$上的表达式;
(2)求$\lim\limits_{x\to+\infty}\dfrac{\int_{0}^{x}f(x)\text{d}t}{x}.$【证】依题意,$f(x)=\text{min}{|x-2k|}(k=0,1,2\cdots)$
当$x\geqslant0$时,
$f(x+2)=\text{min}{|(x+2)-2k|}=\text{min}{|x-2(k-1)|}=f(x)(k=0,1,2\cdots),$故$f(x)$是以2为周期的函数.其在$[0,2]$上的表达式为
$$f(x)=\text{min}{|x-2k|}=\begin{cases}
x,&0\leqslant x<1(k=0),\\2-x,&1\leqslant x\leqslant2(k=1).
\end{cases}$$
故$f(x)$的图像如图所示.(2)【解】当$2n\leqslant x<2n+2$时,
$$n=\int_{0}^{2n}f(t)\text{d}t\leqslant \int_{0}^{x}f(t)\text{d}t\leqslant \int_{0}^{2n+2}f(t)\text{d}t=n+1,$$
故$$\dfrac{n}{2n+2}=\dfrac{1}{2n+2}\int_{0}^{2n}f(t)\text{d}t<\dfrac{1}{x}\int_{0}^{x}f(t)\text{d}t<\dfrac{1}{2n}\int_{0}^{2n+2}f(t)\text{d}t=\dfrac{n+1}{2n},$$
当$x\to+\infty$时,$n\to\infty$,由夹逼准则,有$\lim\limits_{x\to+\infty}\dfrac{\int_{0}^{x}f(x)\text{d}t}{x}=\dfrac{1}{2}.$
可见如何依题意得出周期函数的正确表达式,并通过写成分段函数形式或利用函数图像辅助理解该函数的特性,是利用自变量范围推算积分值范围的先导和关键。
3.2 抽象型
若给出抽象函数求极限,可考虑用单调有界准则:若$x\to+\infty$时,$f(x)$单调增加(减少)且$f(x)$有上界(下界),则$\lim\limits_{x\to+\infty}f(x)$存在.
来看这个引例(摘自《18讲》P11例1.16)
(1)证明:当$x\geqslant1$时,$\dfrac{1}{1+x}<\text{ln}\Big(1+\dfrac{1}{x}\Big)<\dfrac{1}{x}$;
(2)设函数$f(x)$在区间$[1,+\infty)$上连续可导,且$$f^{\prime}(x)=\dfrac{1}{1+f^2(x)}\bigg[\sqrt{\dfrac{1}{x}}-\sqrt{\text{ln}\Big(1+\dfrac{1}{x}\Big)}\bigg].$$
证明:$\lim\limits_{x\to+\infty}f(x)$存在.【证】当$x\geqslant1$时,对$\text{ln}t$在$[x,x+1]$上应用拉格朗日中值定理,有$$\text{ln}(x+1)-\text{ln}(x)=\frac{1}{\xi},x<\xi<x+1,$$即$$\dfrac{1}{x+1}<\text{ln}\Big(1+\dfrac{1}{x}\Big)<\dfrac{1}{x}.$$
(2)由(1)知,$\sqrt{\dfrac{1}{x}}-\sqrt{\text{ln}\Big(1+\dfrac{1}{x}\Big)}>0$,又$\dfrac{1}{1+f^2(x)}>0$,故$f^{\prime}(x)>0$,于是$x\geqslant1$时$f(x)$严格单调增加,又$$f^{\prime}(x)\leqslant \sqrt{\dfrac{1}{x}}-\sqrt{\text{ln}\Big(1+\dfrac{1}{x}\Big)}<\sqrt{\dfrac{1}{x}}-\sqrt{\dfrac{1}{1+x}},$$
上式两边从$1$到$x$积分,有$$\int_{1}^{x}f^{\prime}(x)\text{d}t
= f(x)-f(1)\leqslant \int_{1}^{x}\Big(\sqrt{\dfrac{1}{t}}-\sqrt{\dfrac{1}{1+t}}\Big)\text{d}t
$$$$<\int_{1}^{+\infty}\Big(\sqrt{\dfrac{1}{t}}-\sqrt{\dfrac{1}{1+t}}\Big)\text{d}t
= 2(\sqrt{2}-1),$$
即$$f(x)<2(\sqrt{2}-1)+f(1),$$
故$f(x)$有上界.由单调有界准则,知$\lim\limits_{x\to+\infty}f(x)$存在.
抽象型的极限存在性问题,通常有以下4个步骤:
1.利用题设所给的导函数和原函数的关系得出单调性
2.再次利用导函数和原函数的关系和单调性得出关于导函数的不等式(不等式右边可适当放缩便于后续积分)
3.对不等式两边进行积分,其中导函数的这一边利用牛顿-莱布尼茨公式写成函数值的差,另一边计算积分得出一个存在上界/下界的函数
4.移项得出原函数存在上界/下界
依据这个思路,我们来看下一个例题(摘自《1000题》P7习题14)
设$x\geqslant0$时,$f(x)$满足$f^{\prime}(x)=\dfrac{1}{x^2+f^2(x)}$,且$f(0)=1$,证明:$\lim\limits_{x\to+\infty}f(x)$存在.
【解】由$f^{\prime}(x)>0$可知,$f(x)$单调增加.又$f(0)=1$,所以,当$x\geqslant0$时,$f(x)\geqslant1$,于是有$$f^{\prime}(x)\leqslant\dfrac{1}{1+x^2}(x\geqslant0).$$
于是$$f(x)-f(0)=\int_{0}^{x}f^{\prime}(x)\text{d}t\leqslant\int_{0}^{x}\dfrac{\text{d}t}{1+t^2}=\text{arctan}\space x(x\geqslant0),$$
故$$f(x)\leqslant1+\text{arctan}\space x<1+\dfrac{\pi}{2}.$$
由单调有界准则知,极限$\lim\limits_{x\to+\infty}f(x)$存在.
4 反函数问题
反函数问题较为新颖,目前样本较少。
引例(摘自《1000题》P7习题7)
记$f(x)=27x^3+5x^2-2$的反函数为$f^{-1}$,求极限:$\lim\limits_{x\to\infty}\dfrac{f^{-1}(27x)-f^{-1}(x)}{\sqrt[3]{x}}.$
【解】依题意,显然有$\lim\limits_{x\to\infty}\dfrac{f(x)}{x^3}=27.$
先令$y=f^{-1}(x)$,则$x=f(y)$,且当$x\to\infty$时$y\to\infty$,所以$$\lim\limits_{x\to\infty}\dfrac{f^{-1}(x)}{\sqrt[3]{x}}=\lim\limits_{x\to\infty}\dfrac{y}{\sqrt[3]{f(y)}}=\sqrt[3]{\lim\limits_{x\to\infty}\dfrac{y^3}{f(y)}}=\sqrt[3]{\dfrac{1}{27}}=\dfrac{1}{3}.$$
同理,先令$t=27x$,再令$y=f^{-1}(x)$,则当$x\to\infty$时$t\to\infty$,$y\to\infty$,所以$$\lim\limits_{x\to\infty}\dfrac{f^{-1}(27x)}{\sqrt[3]{x}}=3\lim\limits_{x\to\infty}\dfrac{f^{-1}(t)}{\sqrt[3]{t}}=3\lim\limits_{x\to\infty}\dfrac{y}{\sqrt[3]{f(y)}}=3\sqrt[3]{\lim\limits_{x\to\infty}\dfrac{y^3}{f(y)}}=3\sqrt[3]{\dfrac{1}{27}}=1.$$因此,原式$=1-\dfrac{1}{3}=\dfrac{2}{3}.$
可见,解题的关键在于通过$y=f^{-1}(x)$和$x=f(y)$的变量代换将$\dfrac{f^{-1}(x)}{x}$转变为$\dfrac{y}{f(y)}$,从而进行后续的处理。